April 19, 2006Logistic Growth without Calculus
Kevin has given me an appreciation for what teachers really do. Over Easter weekend I watched him assemble a complete lesson plan with a presentation, examples, activities, handouts, and homework. Much of the work of a teacher is outside the classroom. It is not easy to teach well. When he shared his handouts with me, I realized that teaching logistic growth to tenth graders was an awkward assignment. His math students were pre-calculus, yet the whole idea of sigmoid functions and logistic growth historically came from an analysis of the calculus. Logistic growth is not really a pre-calculus concept. Is it? Sigmoids with Calculus What is logistic growth anyway? Wikipedia provides nice background on it: it is sort of like exponential growth with a ceiling. Recall that exponential growth solves the differential equation where the growth rate is proportional to the value all the way up to infinity. The rich get richer forever and ever. That's how interest in bank accounts work: Logistic growth is a bit different. It solves the differential equation where the growth rate is proportional to a quadratic function that clamps the growth at zero at some limit called the capacity of the system. For example (for a capacity of 1): Pierre Verhulst came up with the idea above when studying population growth (he was trying to understand why we don't all live in a catastrophic Malthusian world). Growth rates can't keep growing forever: in a finite world, there must be finite limits. Once you grow enough, the rules change, and growth slows. Pushing around the integrals to solve Verhulst's differential equation, we get: So the solutions to the differential equation above trace out an S-shaped curve like the canonical sigmoid pictured at the top of this article: The sigmoid is a clean form that is easy to differentiate and so it shows up in lots of places - for example, neural network people like to use it as an alternative to a step function. And it has been popular among people studying population growth or modeling biological systems. Hubbert used it to try to predict a finite limit to global oil production. So logistic functions are everywhere. But you can see that the derivation of the function is all about derivatives, so it seems like a calculusy sort of topic. Sigmoids with Calculators
He began his lesson with the example that the number of iPods sold by Apple might appear to increase by 15% every month. Yet a simple calculation shows they can't increase like that forever. Very quickly you start exceeding crazy numbers like the population of people on the planet. So he showed the kids a form of the sigmoid function and had them use their very high-tech pocket calculators to plot the function numerically to build intuition about it. I was amazed at my brother's use of the calculator in the classroom. He tells me that most high schoolers in the country now use a particular model of Texas Instruments graphing calculators, and most good math teachers weave the devices into the curriculum. Calculators let you make mincemeat out of tricky functions like sigmoids. And why not? In the era of cheap CPU power, kids should get comfortable with doing things numerically. So my brother taught the subject with real numbers, plotting graphs of both the exponential and the sigmoid, and having the kids try to fit the curves to data and compare the results. Did you learn math in the age of the graphing calculator? I did not. Sigmoids with Algebra I If you tried to learn about the sigmoid function without using calculus, you would probably be left with question "where the heck does that formula come from?" Is there a way to understand the mysterious incantation 1/(1 + e-x) without using integration? The answer is "yes." It is easy to understand where the formula comes from without calculus. Yet hunting for internet resources on "logistic growth" doesn't reveal anybody who has discussed a noncalculus justification of the sigmoid anywhere, so here it is. Here is the idea. We know that in the finite world, exponential growth can't continue forever. As dramatic as Apple's music player's success has been, it doesn't make sense for iPod market share to ever exceed 100%. But perhaps Apple can define continuing success in relative terms. (Microsoft, which has enjoyed 95% market share for years, has this problem. How do you motivate a salesman to double his performance when there is no hope of doubling sales next year?) So instead of looking at the market share number by itself, let's try looking at the ratio between the wins and losses. If f is the fraction that we win, then (1 - f) is the portion that we lose, and the win/loss ratio we can use to measure our success is this: If you measure success using the formula above, the game is familiar when you have very small share: you double a small share simply by (approximately) doubling the number of wins. But pass the halfway point and the problem changes its character. Now to get a better score you need to concentrate on reducing the number of losses. The way to double your score when near 100% is to (approximately) halve the number of losses. Even if your winnings cannot grow exponentially, perhaps the ratio between the wins and losses could grow exponentially forever: Is that really possible? Sure! We saw this win/loss ratio in the middle of our calculus derivation before. Using simple algebra to work things out, we get: The last step is arrived at by dividing numerator and demonimator both by ex. So exponential growth in the ratio between wins and losses is possible. The sigmoid function is how it happens. Easy as pie. A case for non-Calculus You might say that the derivation isn't well-motivated. Why look at the win/loss ratio? But people look at win/loss ratios all the time - as any sports fan or day trader will tell you. And to me starting with the win-loss ratio doesn't seem any less motivated than Verhulst's choice of the arbitrary polynomial f(1-f) as the derivative of the growth function. Besides, by understanding the sigmoid as a solution to a win-loss growth function, you get another bonus. The simple math provides direct insight into the general form Whenever you see a function g divided by one plus g, we now know what we are getting. We get a function that describes a proportion between zero and one, and where the ratio between the wins and losses is g(x). If you want to see the ratio to grow linearly, use g(x) = x; or quadratically, use g(x) = x2. It just so happens that the exponential case, the sigmoid where g(x) = ex, comes out to be a particularly pretty function, symmetric around the middle. Something to stick in the mental cupboard. Posted by David at April 19, 2006 11:05 AMComments
Oddly heaplful for my maths assignment. thankyou for sharing :) Posted by: Sarah at March 10, 2007 08:54 PMThank you so much! My daughter Gina (10th grade, in a high school in Germany) had an assignment to explain logistic growth to her classmates. Your site was the only reference we were able to find that explained everything in terms of what the kids already know (algebra) instead of what they have yet to learn. Your clear and easy-to-follow explanation was absolutely wonderful! Many, many, many thanks!! Posted by: Laurie at April 14, 2007 04:27 PMBrilliant!!! Posted by: Brad at January 15, 2008 09:27 PMIf someone needs to calculate the timing hours and activities hour of their employee and ghost employee who is usually working online, then the time calculation is very hard for them. But when they use our Time Card Calculator than this hard calculation becomes easier for them. Posted by: Time Card Calculator at August 13, 2017 09:47 AMIf someone needs to calculate the timing hours and activities hour of their employee and ghost employee who are usually works online, than the time calculation is very hard for them. But when they use our Time Card Calculator than this hard calculation becomes easier for them. Posted by: Time Card Calculator at August 13, 2017 09:48 AMPost a comment
|
| Copyright 2006 © David Bau. All Rights Reserved. |
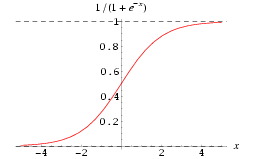 A blog entry about math. My brother
A blog entry about math. My brother 